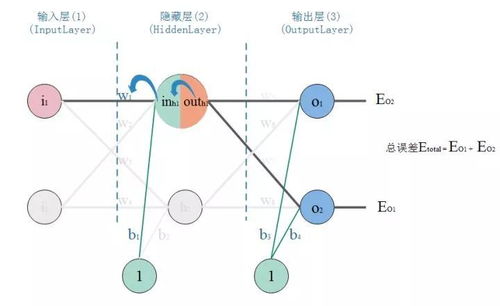
在人工智能的學習道路上,BP(Backpropagation)神經網絡是一個關鍵節點,它結合了算法推導和實際代碼實現,同時離不開數據庫和計算機網絡服務的支持。本文將從入門角度逐步推導BP神經網絡算法,提供Python代碼實現示例,并討論數據庫和網絡服務在AI應用中的角色,幫助讀者避免‘從入門到放棄’的陷阱。\n\n### 一、BP神經網絡算法推導\nBP神經網絡是一種多層前饋網絡,通過誤差反向傳播算法進行訓練。其核心包括前向傳播和反向傳播兩個過程。\n\n1. 前向傳播:輸入數據從輸入層經過隱藏層傳遞到輸出層,計算各層神經元的輸出。設輸入向量為 \( x \),隱藏層輸出為 \( hj = f(\\sumi w{ij} xi + bj) \),其中 \( f \) 是激活函數(如Sigmoid或ReLU),\( w{ij} \) 是權重,\( bj \) 是偏置。輸出層類似計算得到預測值 \( yk \)。\n\n2. 反向傳播:根據預測值與真實值的誤差,反向調整權重和偏置。誤差函數常用均方誤差:\( E = \\frac{1}{2} \\sumk (yk - tk)^2 \),其中 \( tk \) 是目標值。通過鏈式法則計算誤差對權重和偏置的梯度:\n - 輸出層梯度:\( \\frac{\\partial E}{\\partial w{jk}} = (yk - tk) \\cdot f'(netk) \\cdot hj \),其中 \( netk \) 是輸出層凈輸入。\n - 隱藏層梯度:類似計算,誤差從輸出層反向傳播。\n 然后使用梯度下降法更新參數:\( w{ij} = w{ij} - \\eta \\frac{\\partial E}{\\partial w{ij}} \),其中 \( \\eta \) 是學習率。\n\n推導的關鍵在于理解鏈式法則和激活函數的導數,例如Sigmoid函數 \( f(x) = \\frac{1}{1 + e^{-x}} \) 的導數為 \( f'(x) = f(x)(1 - f(x)) \)。\n\n### 二、代碼實現示例(Python)\n以下是一個簡單的BP神經網絡實現,使用Sigmoid激活函數,適用于二分類問題。代碼包括網絡初始化、前向傳播、反向傳播和訓練過程。\n\n`python\nimport numpy as np\n\nclass NeuralNetwork:\n def init(self, inputsize, hiddensize, outputsize):\n self.weights1 = np.random.randn(inputsize, hiddensize)\n self.weights2 = np.random.randn(hiddensize, outputsize)\n self.bias1 = np.zeros((1, hiddensize))\n self.bias2 = np.zeros((1, outputsize))\n \n def sigmoid(self, x):\n return 1 / (1 + np.exp(-x))\n \n def sigmoidderivative(self, x):\n return x * (1 - x)\n \n def forward(self, X):\n self.hidden = self.sigmoid(np.dot(X, self.weights1) + self.bias1)\n self.output = self.sigmoid(np.dot(self.hidden, self.weights2) + self.bias2)\n return self.output\n \n def backward(self, X, y, output, learningrate=0.1):\n error = y - output\n doutput = error * self.sigmoidderivative(output)\n errorhidden = doutput.dot(self.weights2.T)\n dhidden = errorhidden self.sigmoid_derivative(self.hidden)\n \n self.weights2 += self.hidden.T.dot(d_output) learningrate\n self.bias2 += np.sum(doutput, axis=0, keepdims=True) learning_rate\n self.weights1 += X.T.dot(d_hidden) learningrate\n self.bias1 += np.sum(dhidden, axis=0, keepdims=True) * learningrate\n \n def train(self, X, y, epochs=1000):\n for in range(epochs):\n output = self.forward(X)\n self.backward(X, y, output)\n\n# 示例使用\nX = np.array([[0, 0], [0, 1], [1, 0], [1, 1]]) # 輸入數據\nY = np.array([[0], [1], [1], [0]]) # 目標輸出(XOR問題)\n\nnn = NeuralNetwork(2, 4, 1) # 輸入2個節點,隱藏層4個節點,輸出1個節點\nnn.train(X, Y, epochs=10000)\nprint(\
AI從入門到放棄 BP神經網絡算法推導及代碼實現筆記,數據庫與計算機網絡服務
如若轉載,請注明出處:http://www.95ys.cn/product/21.html
更新時間:2026-01-08 03:26:27
產品列表
PRODUCT
----------------